Introduction

Have you ever tried to send a file to a friend who lives far away from you before? How did you send it?

You might decide to send it electronically via email or any social media platform or you decide to transport yourself to your friend's place and hand over the file to your friend physically on a hard drive or an sd card.

Writing an algorithm can also be likened to sending a file to a friend. The way you write your algorithm will determine the time it will take for your algorithm to run just like the method you use to send the file will determine the time it will take for the file to get to your friend's place.

So, what is time complexity?

Time complexity is the time taken for an algorithm to run as a function of the size of its input. This means that we need to take into account different quantities or sizes of input when we write our algorithm.

Have you heard of Big 0?

So, let's go back to the file-sending example above, you might probably conclude that sending the file electronically is the fastest. But, what if the file has a size of 2 terabytes? The amount of time it will take you to send a 2 terabytes file will be much more than the amount of time it will take to send a file that is 200 megabytes in size. In the same way, an algorithm will take different times to complete giving different inputs.

Big 0 is a notation that describes the runtime of an algorithm by its worst runtime (i.e the highest amount of time it takes to run). Other notations are used to describe runtimes like big Ω (big omega) which describes an algorithm's best runtime and big Θ (big theta) which defines an algorithm's average runtime. But, big 0 is the one that is most commonly used in software interviews.

The different big 0 notations

Different big 0 notations can be used to describe the runtime of an algorithm. The four most common big 0 notations are:

• 0(1) - Constant time: an algorithm will take the same number of times for any size of the input).

• 0(log n) - Logarithmic time: the time taken for the algorithm to complete increases very slowly as the input increases.

• 0(n) - Linear time: the algorithm takes proportionally longer to complete as the input grows.

• 0(n^2) - Quadratic time: the time it takes for the algorithm to complete increases exponentially as the input increases.

Below is a graph of the most common big 0 notations.

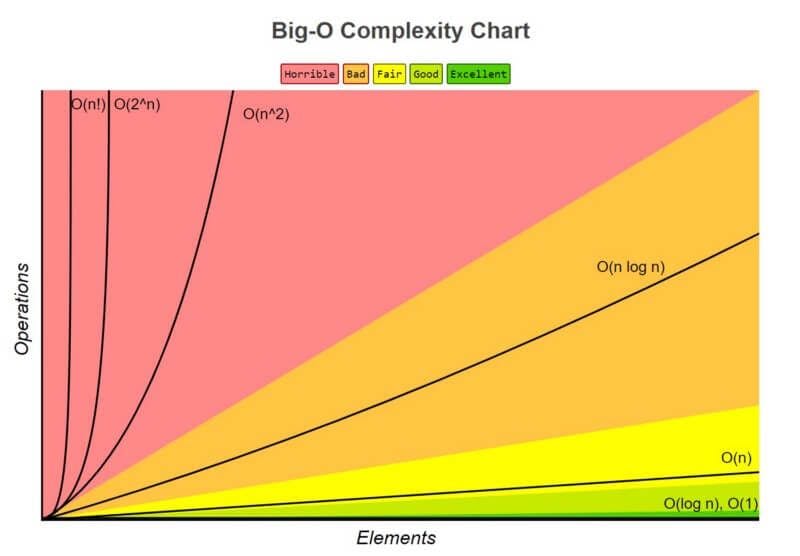
So, what next?

Now that you have learned about the time complexity of an algorithm and big 0, you can learn how to calculate the big 0 of an algorithm so that you can start writing algorithms that are fast and optimized.